When I reached calculus in my senior year of high school, it was clear that it sat atop a mountain that I had been ascending ever since my Algebra 1 class. Without the tools and procedures I had amassed from algebra and precalculus, I could never have performed the symbolic manipulations necessary to differentiate and integrate functions. But how well did I really understand the big ideas of calculus? Only in grad school, while pursuing a degree in math education, did I realize just how fragile my grasp of calculus really was.

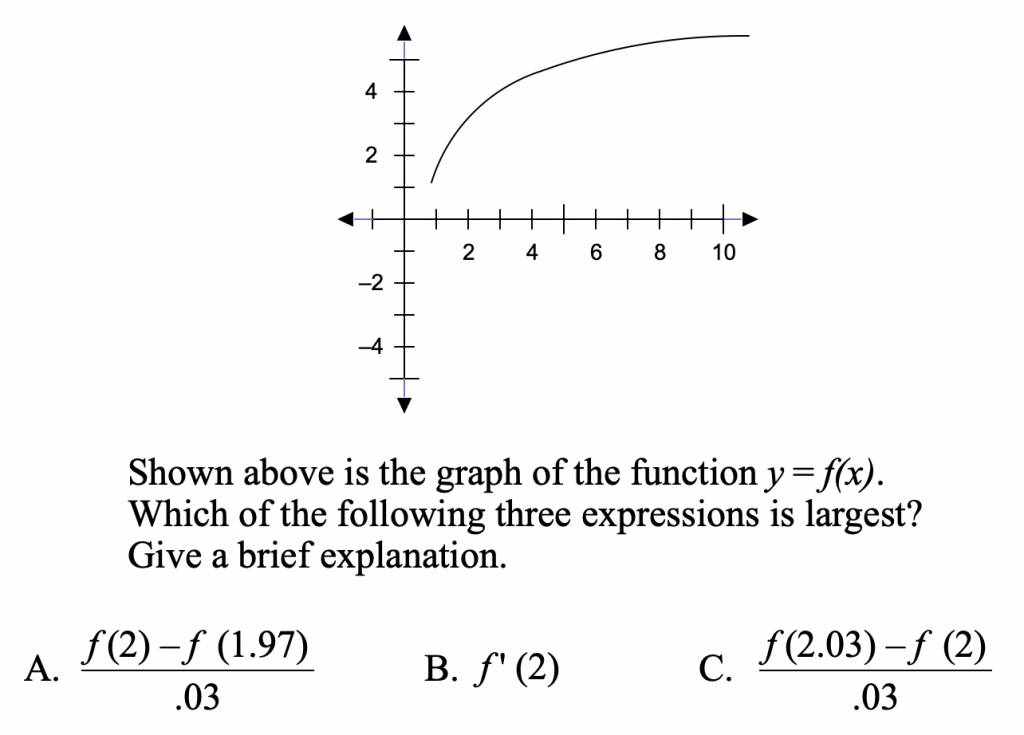
For my master’s thesis, I created a test that assessed how well students understood the conceptual underpinnings of calculus (available here). I borrowed several of my test items from Steven Monk, a mathematician at the University of Washington. Here is one of my favorites:

While some students gave solid arguments for picking option A, others gave explanations that focused on individual points on the graph rather than rate of change. Here are three responses students gave to justify option C:

• f (2.03) is greater than f (1.97) and f (2).
• The y coordinates are larger at the points on the graph.
• When dividing by a fraction, then it’s actually increasing, and f (2.03) is a bigger number.

I came away discouraged by the results of my assessment test, wondering what could be done to help students develop a conceptual understanding of rate of change, slope, and derivatives.

There are many books and videos that do a good job of painting a big-picture overview of calculus, but one of my favorite resource comes from my colleague, Scott. He’s developed a wonderful pair of Web Sketchpad-based activities that focuses on the question, What does it mean to find the slope of the sine function?

The websketch below (and here), along with this worksheet, will get your students started. The video below walks you through the construction steps . Stay tuned as well for next month’s blog post that will present part 2 of this investigation, with a focus on how an algebraic approach can produce a better approximation of the slope.