As a child, I spent many hours (probably too many hours) consuming reruns of television shows from the 1950s and 60s. I Love Lucy was surely the best of the lot, and among its countless comic moments was this one where Lucy, dressed as Harpo Marx, expertly mirrors the real Harpo’s movements.
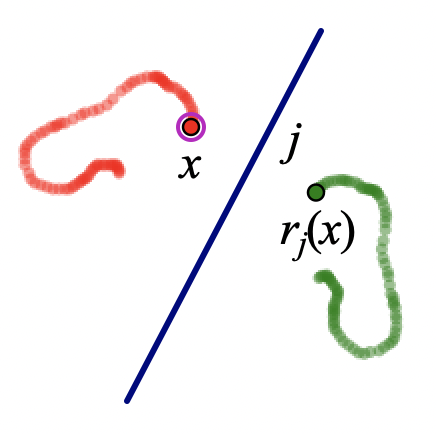
Lucy and Harpo’s reflection routine is a fun introduction to the connections between geometric transformations and functions. A reflection, for example, can be imagined as a function rule r that takes a point x (the independent variable) and reflects it in mirror j to obtain the dependent variable rj(x). Just as the coordinated movement of two people, like Lucy and Harpo, can take the form of a dance, so too we can view the coordinated movement of two points as a function dance; a dance in which the independent point’s location determines the dependent point’s location. Below, as point x is dragged, it leaves behind a red trace of its path. Point rj(x), the reflection of point x in mirror j, simultaneously traces a green path. You can think of these traces as the paths danced by both points.
As part of our NSF-funded Forging Connections project, we asked students to choreograph and then perform their own geometric transformation dances. And not being content to dance in just pairs, students created and performed transformation dances in groups of four.
Cognitive science suggests that students form abstract concepts (such as variable and function) through conceptual metaphors grounded in their experiences. The activities we designed as part of the Forging Connections project provide students with conceptual metaphors both for variables (as students vary their physical location by dancing ) and for functions (as students follow the self-enforced rules of the physical dance). And beyond their connection to variables and functions, the activities are really fun—a far more engaging way to experience geometric transformations than the typical static presentation found in textbooks.
Virtual Dances
Below (and here) is a reflection dance challenge built with Web Sketchpad. You are the dependent variable (the frog), and your goal is to follow the function rule as the penguin moves around her restricted domain. To move correctly, you must always be in the reflected location across the mirror from the penguin. Fortunately you have a reflection segment to help you. When the penguin is in the center of the white cross-hairs, you are in the correct location. The hard part comes when the penguin starts moving: because you’re the dependent variable, you have to move to keep the white cross-hairs centered on the independent variable.
Before you start the game, practice moving the frog so the circle and cross-hairs move around the border of the polygon, because that’s the path that the penguin will dance. When you’re ready to play, move the frog so the cross-hairs are over the penguin. Then press the Ready…Set…Go button and get ready to move the frog. When the countdown ends and the independent variable (the penguin) starts moving, you have to move the dependent variable to always be the reflected image. Both the polygon and the trace will change color, from red to green, when you’re in the right place.
When the independent variable stops dancing, press Check Result to see how you did. If you’re not satisfied with your dance, try it again; you will get better with practice. When you are ready, increase the level of difficulty, or try a different dance (use the page navigation in the lower-right corner to move between dances). To improve your dancing, be aware of the relative rate of change of the two variables: what are their relative speeds and directions? To dance well, your behavior as a dancer must be the same as the mathematical behavior of the function.
On page 1 of the websketch, the mirror is always vertical, but you can drag the vertices of the polygon to create a new dance challenge. On page 2, you can also drag the endpoints of the mirror.
Below (and here) is a similar challenge, but now the dances are based on rotation. On page 3 of websketch, you can decide what angle of rotation to pick and the shape of the polygon.
And finally, below (and here) is a dilation dance where you can change the scale factor and drag the center of dilation and the polygon’s vertices to create new challenges. Pay particular attention to the relative speed and direction of the dancers.
Each of these dances fits in a series of activities in which students are introduced to the specific transformation family, construct it for themselves, analyze its behavior, play transformation games, and dance. Be sure to check out our reflection activities, our rotation activities, and our dilation activities.