At the 2017 NCTM Annual Meeting I was invited to do a short Wednesday-afternoon presentation on Function Dances in the NCTM Networking Lounge. (Here's the handout from the presentation.) The idea of function dances is to get students (or in this case teachers) moving around, acting as the independent and dependent … Continue Reading ››
Revisiting the Isosceles Triangle Challenge
In my last post, I presented a lovely geometry problem from Japan that was ideally suited to a dynamic geometry approach. Below is a new problem whose construction is nearly identical to the original one. The text says, "Five isosceles triangles have their bases on one line, and there are 10 rhombi. One length of the rhombus … Continue Reading ››
A Geometry Challenge from Japan
Here is a wonderful geometry problem from Japan: The five triangles below are all isosceles. The quadrilaterals are all rhombi. The shaded quadrilateral is a square. What is the area of the square?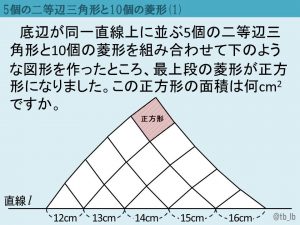 
I wondered at first whether the English translation of the problem was correct because with so many side … Continue Reading ››
I wondered at first whether the English translation of the problem was correct because with so many side … Continue Reading ››Creating Animated Factorization Diagrams
Last year, I had the pleasure of co-organizing a geometry-focused coaching collaborative led by Metamorphosis, a New York-based organization that offers professional content coaching to transform the mindset and practices of teachers and administrators. I had so much fun that I decided to do it again! My workshop partners were Metamorphosis staffers Toni Cameron, Ariel Dlugasch, and … Continue Reading ››
The Varied Paths to Constructing a Square
Using dynamic geometry software, students can use a Segment tool to draw what looks like a square by eyeballing the locations of the vertices. However, the resulting quadrilateral will not stay a square when its vertices are dragged. Building an “UnMessUpAble” square requires that the quadrilateral stay a square when any of its parts are … Continue Reading ››
Make Your Own Fractions
In my very first Sine of the Times blog post from January 2012, I wrote about the paucity of fractions that young learners typically encounter in their math classes. While they might construct visual representations of 1/2, 2/3, and 8/12, it's unlikely they'll create models of 7/31, 36/19, or 5/101. That's a shame because without … Continue Reading ››
Raz’s Magic Multiplying Machine
Here is a question you don't hear very often: What does it feel like to experience multiplication in our bodies? It's a strange question because our typical exposure to multiplication is numerical. I give you two numbers—say, 3 and 5—and you tell me their product, 15. But multiplication need need not be so static and concrete. Back … Continue Reading ››
Pythagoras Plugged In
The title of this post is a nod to the Sketchpad activity module Pythagoras Plugged In by Dan Bennett. Dan's book contains 18 visual, interactive proofs of the Pythagorean Theorem. And there are more: The Pythagorean Proposition, published in 1928 by Elisha Scott Loomis, contains over 350 proofs, 255 of which are geometric. Wow! I revisited the … Continue Reading ››
International Congress for Mathematics Education Part 2
I began this post on Friday night in Hamburg Germany, near the end of ICME, the quadrennial international math-education conference that's been both exhilarating and exhausting. I’m now finishing it on the airplane headed back home. 
As interesting as many of the presentations have been, they've also been … Continue Reading ››
As interesting as many of the presentations have been, they've also been … Continue Reading ››Adding and Subtracting on a Dynamic Number Chart
Below (and here) is a collection of four interactive number charts that we first introduced in our NSF-funded Dynamic Number project. Start by asking students to press the four directional arrows and to explore what they do. The right arrow, for example, moves the shaded square to the right, and wraps the square to the next row up … Continue Reading ››