 My first thought was that surely the problem was … Continue Reading ››
My first thought was that surely the problem was … Continue Reading ››A Geometry Gem from Twitter
 My first thought was that surely the problem was … Continue Reading ››
My first thought was that surely the problem was … Continue Reading ›› My first thought was that surely the problem was … Continue Reading ››
My first thought was that surely the problem was … Continue Reading ››What would it take to build a better number grid for young learners? A typical number grid contains 10 columns with the numbers progressing from 1-10, 11-20, 21-30 and so on, from row to row. We decided to upend this tradition and make a dynamic number grid with Web Sketchpad that allows students to … Continue Reading ››
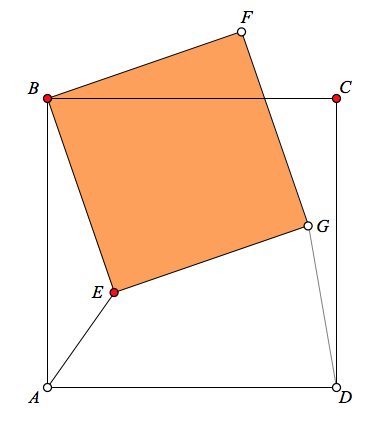
In the interactive Web Sketchpad model below (and here), ABCD is an arbitrary quadrilateral whose midpoints form quadrilateral EFGH. Drag any vertex of ABCD. What do you notice about EFGH?
The midpoint quadrilateral theorem, attributed to the French mathematician Pierre Varignon, is relatively new in the canon of geometry theorems, dating to 1731. Mathematics educator Chris Pritchard says … Continue Reading ››
At the 2017 NCTM Annual Meeting I was invited to do a short Wednesday-afternoon presentation on Function Dances in the NCTM Networking Lounge. (Here's the handout from the presentation.)
The idea of function dances is to get students (or in this case teachers) moving around, acting as the independent and dependent … Continue Reading ››