In the fall of 2023, I taught a geometry methods course at City College here in New York. While my goal was to make use of Web Sketchpad throughout the semester, I knew that the most effective use of the software required activities that coupled it with hands-on modeling. Two such opportunities arose … Continue Reading ››
All posts by Daniel Scher
Tracing the Sine and Cosine Functions
How might we help students connect the unit-circle representation of trigonometric functions with the graphs of these same functions? Below (and here) is a Web Sketchpad model that gives students the tools to construct the graphs of trigonometric functions by using the unit circle as the driving engine. To get started, … Continue Reading ››
Constructing Daisy Designs
With nothing but a compass, students can construct a lovely daisy design consisting of seven interlocking circles, all of the same size.
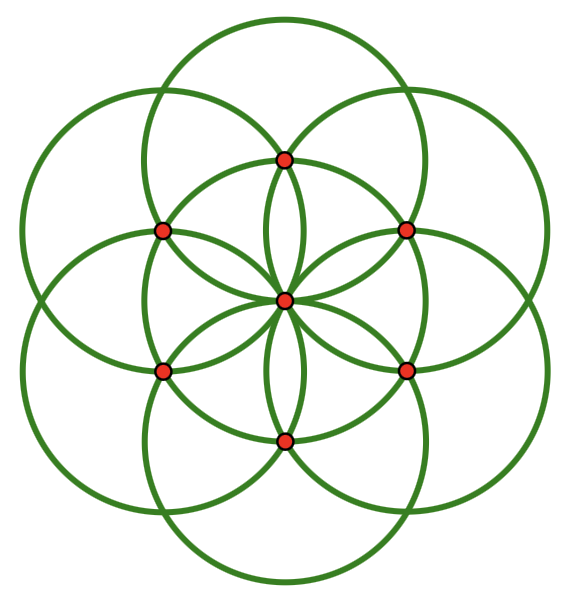
I was delighted to see that the U.S. postal service chose to feature … Continue Reading ››
Slope Games Aplenty
Eleven years ago, I wrote a post titled What is All the Fuss About Lines? In it, I discussed the difficulties that students encounter when asked to determine the equation of a line. Faced with formulas for calculating slope, the point-slope form of a line, and the slope-intercept form, students lose … Continue Reading ››
The Mysteries of Polygon Flats
What do you get when you cross geometry with the classic murder mystery game Clue? Why, the Mysteries of Polygon Flats, of course!
In my prior post, I offered examples of how Web Sketchpad can help students classify special quadrilaterals like squares, rectangles, kites, parallelograms, … Continue Reading ››
Classifying Quadrilaterals
Ah geometry, how you suffer from a lack of attention in the elementary grades! Rare is the curriculum that doesn't stuff geometry into its final chapter, waiting patiently in line behind number and operation.
But the one geometry topic that does command attention is classifying two-dimensional shapes into … Continue Reading ››
A Geometric Interpretation of Euler’s Identity
While most numbers lead anonymous lives away from the mathematical spotlight, eiπ occupies hallowed ground. Douglas Hofstadter writes that when he first saw the statement eiπ = −1, “. . . perhaps at age 12 or so, it seemed truly magical, almost other-worldly.”
At the risk of deflating the celebrity status of … Continue Reading ››
Teaching with Web Sketchpad
This past semester, I taught a geometry course for teachers at City College here in New York. As you might expect, Sketchpad figured heavily in the course contents. But unlike other semesters when desktop Sketchpad was my tool of choice, this time, I took the plunge and limited myself to Web Sketchpad.
A Transformations Approach to Complex Numbers
This post, inspired by the work of Al Cuoco, uses Web Sketchpad to explore a transformations approach to complex numbers.
Slope of the Sine Function, Part 2
In my previous post, I presented a non-algebraic approach to exploring the slope of the sine function. That method involved placing a secant line on the graph and then dragging the two points that defined the line as close together as possible to approximate the tangent line.
By dragging, … Continue Reading ››