Students often have difficulty connecting the Cartesian graph of a function to the actual motion of the variables. Their challenge in visualizing and describing covariation (the way y varies as x varies steadily) relates to their understanding of function families: function families are distinguished by the nature of their covariation. A function whose growth rate remains constant … Continue Reading ››
All posts by Daniel Scher
Pattern Block Puzzles
Several days ago, I was reminded of an interactive pattern block puzzle that I designed during the pandemic in collaboration with Toni Cameron of Reimagined. It provides an engaging opportunity to promote proportional reasoning in the context of geometry.
On page 1 of the websketch below (and Continue Reading ››
Some Triangle Shearing Investigations
When I taught a geometry methods course at City College last fall, I devoted an entire class to investigating area. We focused on problems where triangles were sheared, transforming into new triangles, but maintaining their area. The two Web Sketchpad activities that follow introduce shearing and present a problem with a surprising result … Continue Reading ››
Maximizing Triangle Area
In the February 1954 issue of Mathematics Teacher, Paul C. Clifford describes an optimization problem from his trigonometry class. Of all isosceles triangles ABC with sides AB and BC of length 12, which one has the maximal area? Clifford told his class that an exact solution to the question required calculus. One student, … Continue Reading ››
Constructing Rectangles with Constant Perimeter and Constant Area
In the fall of 2023, I taught a geometry methods course at City College here in New York. While my goal was to make use of Web Sketchpad throughout the semester, I knew that the most effective use of the software required activities that coupled it with hands-on modeling. Two such opportunities arose … Continue Reading ››
Tracing the Sine and Cosine Functions
How might we help students connect the unit-circle representation of trigonometric functions with the graphs of these same functions? Below (and here) is a Web Sketchpad model that gives students the tools to construct the graphs of trigonometric functions by using the unit circle as the driving engine. To get started, … Continue Reading ››
Constructing Daisy Designs
With nothing but a compass, students can construct a lovely daisy design consisting of seven interlocking circles, all of the same size.
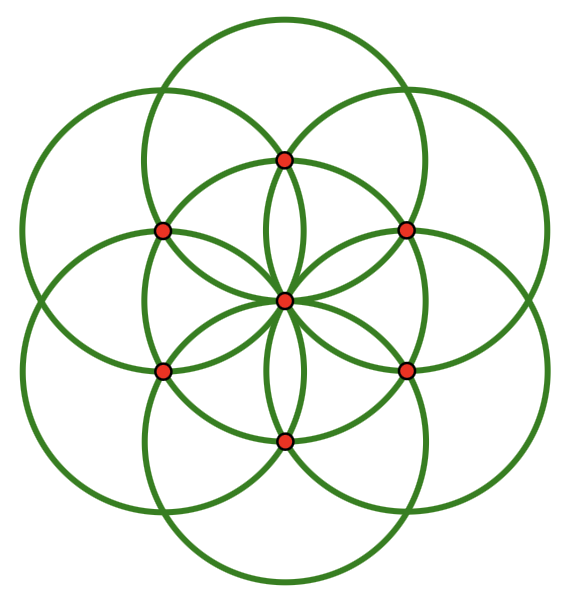
I was delighted to see that the U.S. postal service chose to feature … Continue Reading ››
Slope Games Aplenty
Eleven years ago, I wrote a post titled What is All the Fuss About Lines? In it, I discussed the difficulties that students encounter when asked to determine the equation of a line. Faced with formulas for calculating slope, the point-slope form of a line, and the slope-intercept form, students lose … Continue Reading ››
The Mysteries of Polygon Flats
What do you get when you cross geometry with the classic murder mystery game Clue? Why, the Mysteries of Polygon Flats, of course!
In my prior post, I offered examples of how Web Sketchpad can help students classify special quadrilaterals like squares, rectangles, kites, parallelograms, … Continue Reading ››
Quadrilateral Pretenders
Ah geometry, how you suffer from a lack of attention in the elementary grades! Rare is the curriculum that doesn't stuff geometry into its final chapter, waiting patiently in line behind number and operation.
But the one geometry topic that does command attention is classifying two-dimensional shapes into … Continue Reading ››