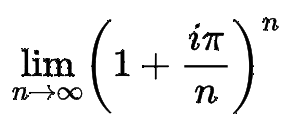While most numbers lead anonymous lives away from the mathematical spotlight, e^iπ  occupies hallowed ground. Douglas Hofstadter writes that when he first saw the statement e^iπ = −1, “. . . perhaps at age 12 or so, it seemed truly magical, almost other-worldly.”

At the risk of deflating the celebrity status of e^iπ, what follows is an intuitive, dynamic geometry interpretation described in The Book of Numbers by John Conway and Richard Guy.

Written as a limit, e^iπ is equal to the following:

Let’s start small and evaluate (1 + iπ/n)ⁿ for n = 8. And rather than use algebra, we can instead approach the computation geometrically: given two complex numbers, z and w, the argument of zw is the sum of the arguments of z and w, and length of zw is the product of the lengths of z and w. (For more information and a proof, see this prior blog post.)

In the sketch below, point B represents (1 + iπ/8) in the complex plane. By measuring ∠AOB (its argument) and OB (its length), we can construct (1 + iπ/8)², (1 + iπ/8)³, … all the way up to (1 + iπ/8)⁸ by using desktop Sketchpad’s iteration feature. Point P, whose location is reported as –1.7554 + 0.262i, represents (1 + iπ/8)⁸.

Now drag slider point n to the right. When n = 130, we see that point P, which represents (1 + iπ/130)¹³⁰, is equal to –1.0387 + 0.001i. Not bad for a rough approximation of e^iπ!

Note that for large n, ∆BOA closely approximates a circle sector with arc length π/n. As there are n stacked triangles in the final product, it makes sense that point P should nearly lie on the negative real axis. The length of OB is (1 + π²/n²)^0.5, and so OP is (1 + π²/n²)^0.5n. Graphing this expression, entering large n values on a calculator, or using a little calculus suggest OP approaches 1 as n grows infinite. Thus, combining the angle and length observations leads to the conclusion that point P, our e^iπ approximation, nears –1 for large n.