Several weeks ago, Dan Meyer described his experience of completing 88 practice sets in Khan Academy’s eighth-grade online mathematics course. His goal was to document the types of evidence the Khan Academy asked students to produce of their mathematical understanding. Dan’s findings were disappointing: He concludes that 74% of the Khan Academy’s eighth-grade questions were either multiple choice or required nothing more than a numerical response.

By contrast, Dan notes that the Smarter Balanced Assessment Consortium (SBAC) has a stronger focus on questions that ask students to “construct,” “analyze,” and “argue” as a way to test their understanding of Common Core mathematics. A Khan Academy diet of multiple-choice items and numeric answers would seem ill suited to helping students prepare for the types of mathematical reasoning expected by the Common Core.

What might explain the mismatch between the Khan Academy’s offerings and the demands of the Common Core? Dan Meyer’s answer is a practical one: Our ability to assess students’ mathematical understanding with technology is primitive. He explains, “Khan Academy asks students to solve and calculate so frequently, not because those are the mathematical actions mathematicians and math teachers value most, but because those problems are easy to assign with a computer in 2014. Khan Academy asks students to submit their work as a number or a multiple-choice response, not because those are the mathematical outputs mathematicians and math teachers value most, but because numbers and multiple-choice responses are easy for computers to grade in 2014.”

Dan’s comments about the difficulty of authoring rich, computer-gradable mathematics tasks reminded me of work that Steve Rasmussen, Scott Steketee, Nick Jackiw, and I undertook several years ago. We set out to discover whether Sketchpad could deliver assessment items that would engage students in dynamic mathematical models and have them demonstrate their understanding through their interactions with the models. Starting with this blog post and in the next two or three to follow, I’ll share some of our assessment ideas.

I’ll state upfront that our examples are not revolutionary—these are mathematical tasks that are several notches above numerical answers and multiple-choice responses, but they’re still based on traditional content. Nonetheless, they are representative of what can be done now with Web Sketchpad, and they point the way to more ambitious possibilities.

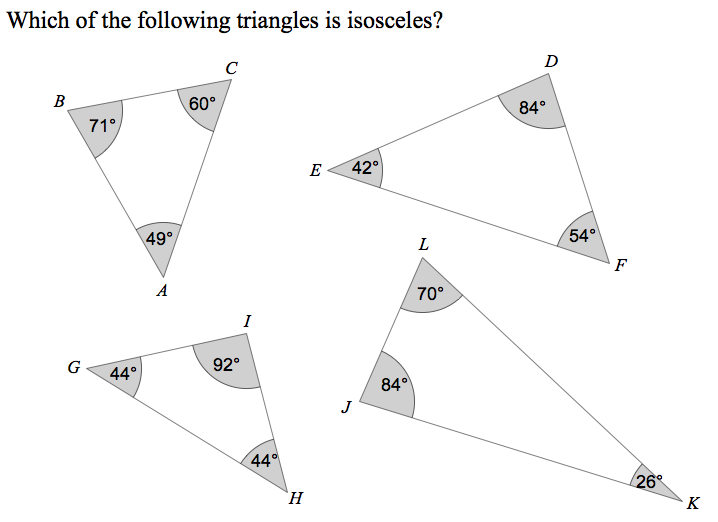
I’ll start with a question that assesses students’ basic understanding of isosceles triangles. Read the multiple-choice item below. It’s a straightforward question, and if a student knows the definition of an isosceles triangle, there isn’t any thinking required. Indeed, even if a student knows nothing about isosceles triangles, she might still pick the correct triangle, as only one triangle visibly differs from the others in having two of its angles equal.

Now, consider the assessment task below. It again centers on the fundamental definition of an isosceles triangle, but it is different from its static counterpart above. Rather than pick which of four triangles is isosceles, students are given a single triangle—one whose lengths and angles can be changed by dragging its vertices—and are asked to make it isosceles. The multiple-choice question had just one right answer; this dynamic version yields numerous solutions. Any isosceles triangle the student creates, whether it be one with angle measures 2°, 2°, and 176° or 50°, 50°, and 80°, counts as correct.

When compared to the passivity of identifying an isosceles triangle, the engagement required to make an isosceles triangle feels like a step up on the assessment ladder. But with better assessments comes the question of how we should grade them. The multiple-choice version is clear enough—a student’s answer is either right or wrong with no room for partial credit. But grading the dynamic version is thornier. Answering the question requires a student to use a mouse, a trackpad, or perhaps her finger to position the triangle’s vertices. Try this yourself with the Web Sketchpad model above. It can be surprisingly tricky to get the triangle’s angles to match the values you have in mind!

The motor skills needed to adjust the angles precisely led us to factor in some forgiveness to the scoring, shown below. If a student drags the triangle so that two angles are either 1 or 2 degrees apart, we award him partial credit and the benefit of the doubt, assuming that his unrealized goal was to create two congruent angles.

Are we too generous? Perhaps. But if a computer-based assessment item makes genuine use of the opportunities offered by technology (dragging, constructing, measuring, etc.) then we have to consider whether students have enough exposure to the technology prior to the test so that the assessment measures their mathematical understanding and not their proficiency with the software (Of course, if the assessment is grounded in poorly designed software, then no degree of practice may make a difference!)

Finally, imagine taking this isosceles triangle item to the next level of assessment sophistication. Rather than provide students with a triangle, we start them with a blank screen and a circle and segment tool. Using these tools, their goal is to construct a triangle that stays isosceles no matter how its vertices are dragged. This is a great example of a meaningful construction task, but it raises several questions:

1. Will Common Core curricula commit to making computer-based constructions a part of their content?
2. Can teachers devote enough time to such construction tasks so that students are prepared for them when assessed?
3. Can we find a way for computers to grade construction tasks?

I’m curious to hear what you think!